Hace un tiempo que vengo estudiando algoritmos y estructuras de datos, el fin es simplemente fortalecer las bases, y algo que venía pateando es Big (O) notation. Así que decidí hacer este post para reflejar lo que voy aprendiendo, tal vez lo vaya actualizando.

Introducción

Básicamente lo usamos para describir la eficiencia de algoritmos en términos de su crecimiento relativo. Se usa este símbolo en la teoría de la complejidad, la informática y las matemáticas para describir el comportamiento asintótico de las funciones, que es básicamente cómo una función o algoritmo se comporta o crece cuando su input (n) tiende a valores muy grandes.

Ejemplo de función:

T(n) = 4n2 − 2n + 2

4nˆ2 domina el crecimiento de la función por eso podemos decir que:

T(n) = O(n2)

Básicamente te dice cuan rápido crece o declina una función. Se utiliza la letra O porque la tasa de crecimiento de una función también se llama su orden.

La definición en CS puede diferir un poco de la de matemática, ya que los algoritmos siempre trabajan con tamaños de entrada que no pueden ser negativos, es decir, no existe una lista de tamaño -5.

Acá hay una lista de clases de funciones que te podes encontrar comúnmente analizando algoritmos.

O(1) por ejemplo es de tiempo constante, siempre tarda lo mismo sin importar la entrada (tamaño), si un algoritmo crece más lento es más eficiente.

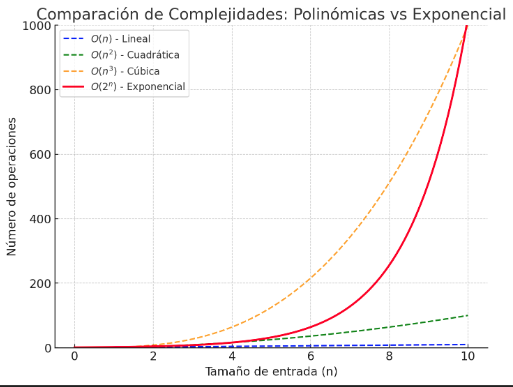
Lo primero que podemos ver de antemano es que O(nc) se parece mucho a O(cn) pero hay grandes diferencias entre la polinómica y la exponencial.

O(nc) (polinómico)

• Crece como una potencia de n, donde c es constante.

• Crecimiento moderado: si N aumenta la función crece, pero controlada.

O(cn) (exponencial)

• Crece como una base constante elevada a la n.

• Crecimiento muchísimo más exponencial: incluso con valores pequeños de c, la función explota rápidamente cuando n aumenta.

• Exponencial siempre es peor que polinómico.

O(1) (constante)

No cambia con n, siempre tarda lo mismo.

function accesoDirecto (arr) {
	return arr[0]; // Siempre accede al primer elemento
}

• No hay bucles ni recursión.

• Operaciones simples como acceder a un index de un array, hacer una suma o asignación.

• Si el array tiene 10 elementos = una operación.

• Si el array tiene 1000 elementos = una operación.

Siempre tarda lo mismo.

O(log(n)) (logaritmica)

• El problema se reduce en cada operación.

function busquedaBinaria(arr, objetivo) {
  let inicio = 0,
    fin = arr.length - 1

  while (inicio <= fin) {
    let medio = Math.floor((inicio + fin) / 2)

    if (arr[medio] === objetivo) {
      return medio // Encontrado, devuelve index
    } else if (arr[medio] < objetivo) {
      inicio = medio + 1 // Buscar en la mitad derecha
    } else {
      fin = medio - 1 // Buscar en la mitad izquierda
    }
  }

  return -1 // No encontrado
}

Array de 1000 elementos = ~10 ops.

Array de 1 000 000 elementos = ~20 ops.

Ej: búsqueda binaria.

• La curva de tiempo desacelera.

O(n) (tiempo lineal)

• Cada elemento se recorre al menos una vez.

• El tiempo de ejecución crece proporcionalmente al tamaño de la entrada.

function recorrerLista(arr) {
  for (let i = 0; i < arr.length; i++) {
    console.log(arr[i]);  // Se ejecuta 1 vez por cada elemento
  }
}

• Array de 1000 elementos = 1000 ops.

• Array de 1 000 000 elementos = 1 000 000 ops.

Ej: Buscar usuario en una lista sin ordenar.

Si tuviese dos bucles iguales sería O(2n):

function recorrerLista(arr) {
  for (let i = 0; i < arr.length; i++) {
    console.log(arr[i]);  // Se ejecuta 1 vez por cada elemento
  }
  
  for (let i = 0; i < arr.length; i++) {
    console.log(arr[i]);  // Se ejecuta 1 vez por cada elemento
  }
}

O(n) + O(n) = O(2n)

O(n2) (tiempo cuadrático)

• Cada elemento se compara con todos los demás elementos.

• Mucho más lento que

function compararPares(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length; j++) {
      console.log(arr[i], arr[j]); // Dos bucles anidados → complejidad cuadrática
    }
  }
}

• Array tiene 10 elementos = 100 ops.

• Array tiene 100 elementos = 10k ops.

• Bucles anidados, bubble sort etc.

Ej: Comparar c/ usuario con todos los demás en una red social.

O(nc) (tiempo polinómico)

• Peor que el cuadrático, pero no que el exponencial.

• Se suele usar en grafos.

function mostrarCombinaciones(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length; j++) {
      for (let k = 0; k < arr.length; k++) {
        console.log(arr[i], arr[j], arr[k]); // Tres bucles anidados → cúbico
      }
    }
  }
}

• Array 1000 elementos = 1 000 000 000 ops.

• Tres bucles o más anidados

• Algoritmo Floyd-warshall (grafos)

O(cn) (tiempo exponencial)

• El tiempo se pone muy exponencial muy rápido.

• El peor tipo de complejidad, solo valido para n muy chicos.

• c (operaciones x entrada) elevado al numero de entradas n

function fibonacci(n) {
  if (n <= 1) return n;
  return fibonacci(n - 1) + fibonacci(n - 2); // Se llama a sí misma dos veces por cada ejecución
}

O(2n) son dos nuevas llamadas recursivas por cada llamada a la función.

Eficiencia

Para terminar me gustaría hablar un poco de eficiencia de algoritmos, ya que, en realidad abarca muchos recursos:

• CPU (time) usage

• Memory usage

• Disk usage

• Network usage

Y a veces se suele confundir performance con complejidad que es lo explicado en este post.

La performance es cuanto tiempo, memoria etc. utiliza un programa al ejecutarse, esto depende mucho del hardware, compilador, lenguaje, optimizaciones etc.

Ej: mismo programa en pc potente (1 seg) vs pc lento (10 segs) eso es el rendimiento / performance.

Por otro lado, la complejidad se refiere a cómo escala el tiempo (u otro recurso) necesario al crecer el problema. Cómo afecta el tamaño del problema al tiempo requerido, la complejidad no depende del hardware.